Need help? We're here to assist you!
Thank You for Enquiry, we will contact you soon!
Close
The Class 7 is an important year in a student’s life and Maths is one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 7 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete NCERT Class 7 Maths Book syllabus.

Exercise 10.1 Page: 196
1. Draw a line, say AB, take a point C outside it. Through C, draw a line parallel to AB using ruler and compasses only.
Solution:-
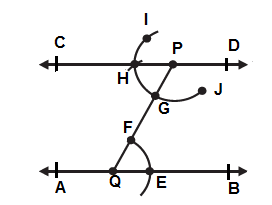
Steps for construction
1. Draw a line AB.
2. Take any point Q on AB and a point P outside AB and join PQ.
3. With Q as the centre and any radius, draw an arc to cut AB at E and PQ at F.
4. With P as the centre and the same radius, draw an arc IJ to cut QP at G.
5. Place the pointed tip of the compass at E and adjust the opening so that the pencil tip is at F.
6. With the same opening as in step 5 and with G as the centre, draw an arc cutting the arc IJ at H.
7. Now, join PH to draw a line CD.
2. Draw a line L. Draw a perpendicular to L at any point on L. On this perpendicular, choose a point X, 4 cm away from l. Through X, draw a line m parallel to L.
Solution:-
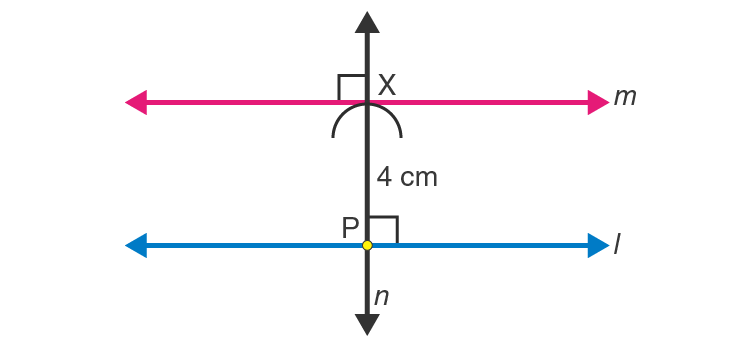
Steps for construction
1. Draw a line L.
2. Take any point P on line L.
3. At point P, draw a perpendicular line N.
4. Place the pointed tip of the compass at P and adjust the compass up to length of 4 cm, draw an arc to cut this perpendicular at point X.
5. At point X, again draw a perpendicular line M.
3. Let L be a line and P be a point not on L. Through P, draw a line m parallel to L. Now join P to any point Q on L. Choose any other point R on m. Through R, draw a line parallel to PQ. Let this meet L at S. What shape do the two sets of parallel lines enclose?
Solution:-
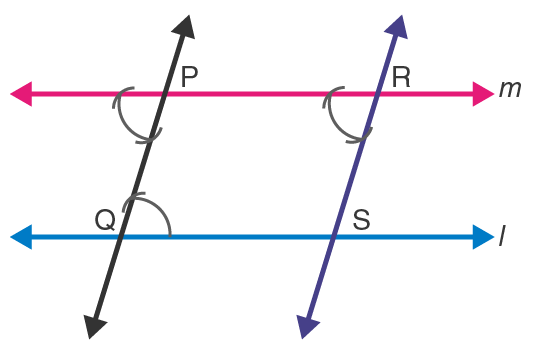
Steps for construction
1. Draw a line L.
2. Take any point Q on L and a point P outside L and join PQ.
3. Make sure that angles at point P and point Q are equal, i.e., ∠Q = ∠P
4. At point P, extend the line to get line M which is parallel L.
5. Then take any point R on line M.
6. At point R, draw an angle such that ∠P = ∠R.
7. At point R, extend the line which intersects line L at S and draw a line RS.
Exercise 10.2 Page: 199
1. Construct ΔXYZ in which XY = 4.5 cm, YZ = 5 cm and ZX = 6 cm.
Solution:-
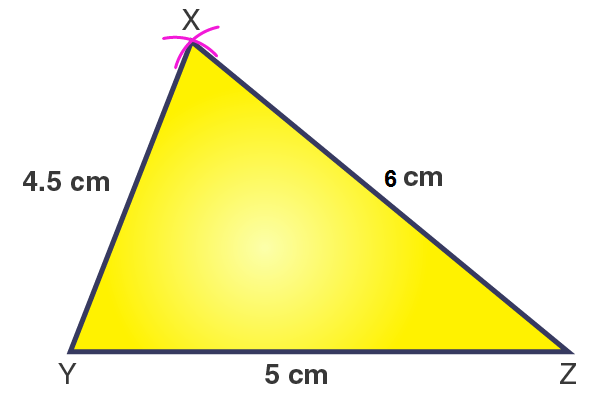
Steps of construction
1. Draw a line segment YZ = 5 cm.
2. With Z as a centre and radius 6 cm, draw an arc.
3. With Y as a centre and radius 4.5 cm, draw another arc, cutting the previous arc at X.
4. Join XY and XZ.
Then, ΔXYZ is the required triangle.
2. Construct an equilateral triangle of side 5.5 cm.
Solution:-
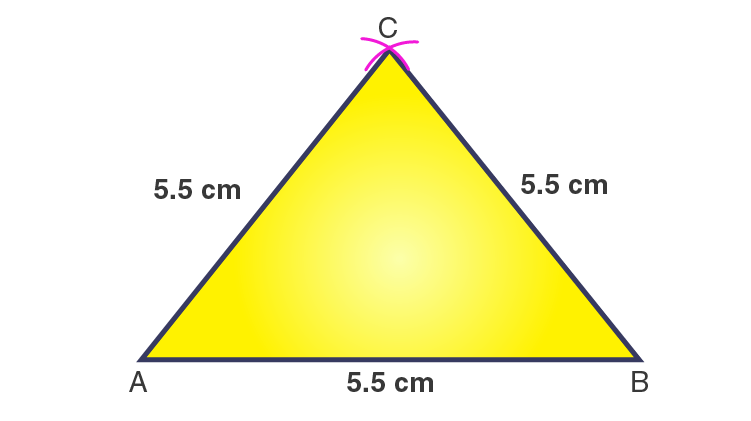
Steps of construction
1. Draw a line segment AB = 5.5 cm.
2. With A as a centre and radius 5.5 cm, draw an arc.
3. With B as a centre and radius 5.5 cm, draw another arc, cutting the previous arc at C.
4. Join CA and CB.
Then, ΔABC is the required equilateral triangle.
3. Draw ΔPQR with PQ = 4 cm, QR = 3.5 cm and PR = 4 cm. What type of triangle is this?
Solution:-
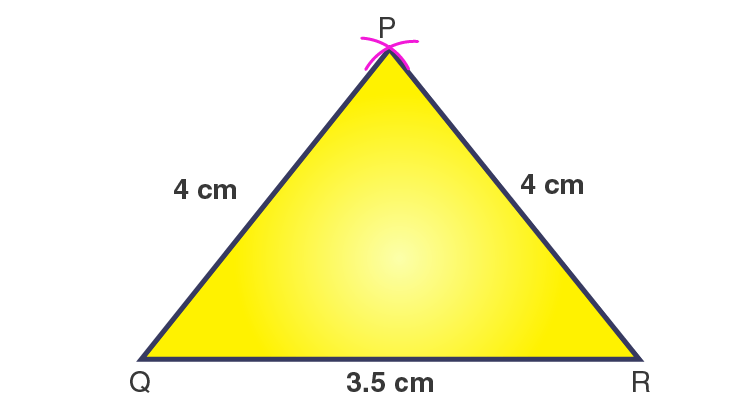
Steps of construction
1. Draw a line segment QR = 3.5 cm.
2. With Q as a centre and radius 4 cm, draw an arc.
3. With R as a centre and radius 4 cm, draw another arc, cutting the previous arc at P.
4. Join PQ and PR.
Then, ΔPQR is the required isosceles triangle.
4. Construct ΔABC, such that AB = 2.5 cm, BC = 6 cm and AC = 6.5 cm. Measure ∠B.
Solution:-
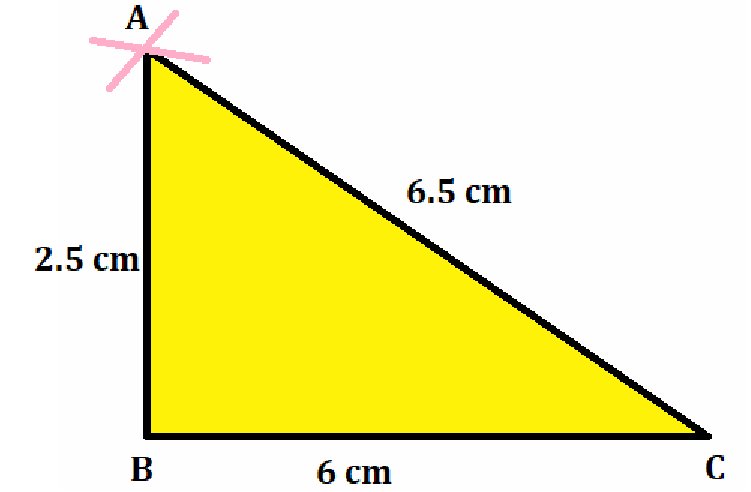
1. Draw a line segment BC = 6 cm.
2. With B as a centre and radius 2.5 cm, draw an arc.
3. With C as a centre and radius 6.5 cm, draw another arc, cutting the previous arc at A.
4. Join AB and AC.
Then, ΔABC is the required triangle.
5. When we will measure the angle B of triangle by a protractor, the angle is equal to ∠B = 90o
Exercise 10.3 Page: 200
1. Construct ΔDEF such that DE = 5 cm, DF = 3 cm and m∠EDF = 90o .
Solution:-
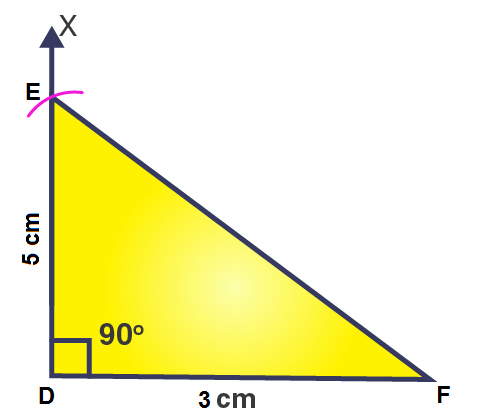
Steps of construction
1. Draw a line segment DF = 3 cm.
2. At point D, draw a ray DX to making an angle of 90o, i.e., ∠XDF = 90o .
3. Along DX, set off DE = 5cm.
4. Join EF.
Then, ΔEDF is the required right-angled triangle.
2. Construct an isosceles triangle in which the lengths of each of its equal sides is 6.5 cm and the angle between them is 110o .
Solution:-
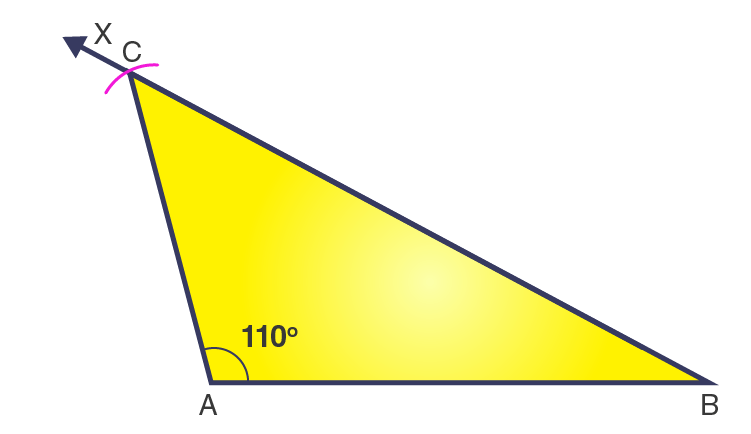
Steps of construction
1. Draw a line segment AB = 6.5 cm.
2. At point A, draw a ray AX to making an angle of 110o , i.e., ∠XAB = 110o .
3. Along AX, set off AC = 6.5cm.
4. Join CB.
Then, ΔABC is the required isosceles triangle.
3. Construct ΔABC with BC = 7.5 cm, AC = 5 cm and m∠C = 60°.
Solution:-

Steps of construction
1. Draw a line segment BC = 7.5 cm.
2. At point C, draw a ray CX to making an angle of 60o , i.e., ∠XCB = 60o .
3. Along CX, set off AC = 5cm.
4. Join AB.
Then, ΔABC is the required triangle.
Exercise 10.4 Page: 202
1. Construct ΔABC, given m ∠A =60o , m ∠B = 30o and AB = 5.8 cm.
Solution:-
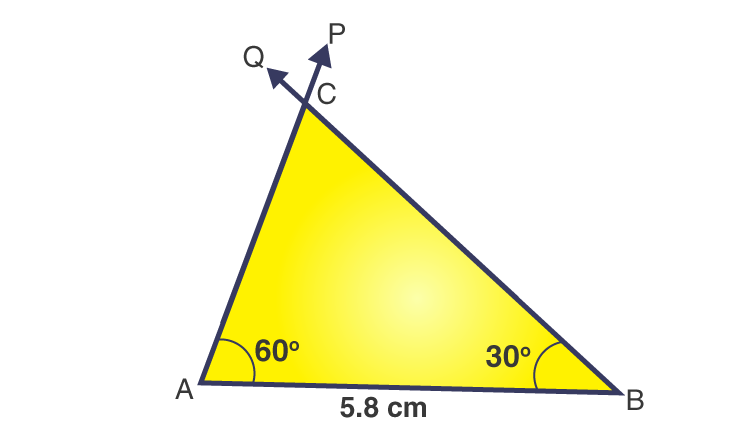
Steps of construction:
1. Draw a line segment AB = 5.8 cm.
2. At point A, draw a ray P to making an angle of 60o , i.e., ∠PAB = 60o .
3. At point B, draw a ray Q to making an angle of 30o , i.e., ∠QBA = 30o .
4. Now, the two rays – AP and BQ – intersect at point C.
Then, ΔABC is the required triangle.
2. Construct ΔPQR if PQ = 5 cm, m∠PQR = 105o and m∠QRP = 40o .
(Hint: Recall angle-sum property of a triangle).
Solution:-
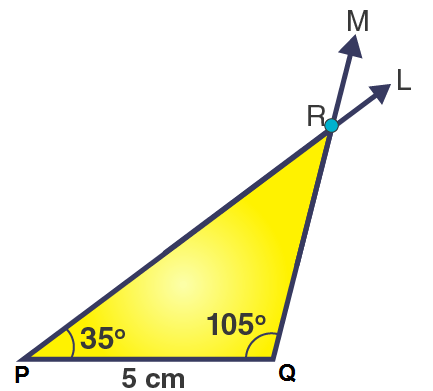
We know that the sum of the angles of a triangle is 180o .
∴ ∠PQR + ∠QRP + ∠RPQ = 180o
= 105o + 40o + ∠RPQ = 180o
= 145o + ∠RPQ = 180o
= ∠RPQ = 180o – 1450
= ∠RPQ = 35o
Hence, the measures of ∠RPQ is 35o .
Steps of construction
1. Draw a line segment PQ = 5 cm.
2. At point P, draw a ray L to making an angle of 105o , i.e., ∠LPQ = 35o .
3. At point Q, draw a ray M to making an angle of 40o , i.e., ∠MQP = 105o .
4. Now, the two rays – PL and QM – intersect at point R.
Then, ΔPQR is the required triangle.
3. Examine whether you can construct ΔDEF, such that EF = 7.2 cm, m∠E = 110° and m∠F = 80°. Justify your answer.
Solution:-
From the question, it is given that
EF = 7.2 cm
∠E = 110o
∠F = 80o
Now, we have to check whether it is possible to construct ΔDEF from the given values.
We know that the sum of the angles of a triangle is 180o .
Then,
∠D + ∠E + ∠F = 180o
∠D + 110o + 80o = 180o
∠D + 190o = 180o
∠D = 180o – 1900
∠D = -10o
We may observe that the sum of two angles is 190o is greater than 180o . So, it is not possible to construct a triangle.
Exercise 10.5 Page: 203
1. Construct the right-angled ΔPQR, where m∠Q = 90°, QR = 8cm and PR = 10 cm.
Solution:-
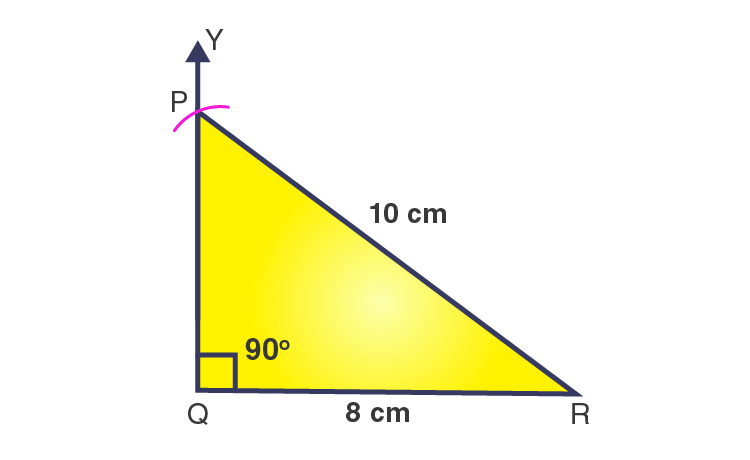
Steps of construction
1. Draw a line segment QR = 8 cm.
2. At point Q, draw a ray QY to making an angle of 90o , i.e., ∠YQR = 90o .
3. With R as a centre and radius 10 cm, draw an arc that cuts the ray QY at P.
4. Join PR.
Then, ΔPQR is the required right-angled triangle.
2. Construct a right-angled triangle whose hypotenuse is 6 cm long and one of the legs is 4 cm long
Solution:-
Let us consider ΔABC is a right-angled triangle at ∠B = 90o
Then,
AC is hypotenuse = 6 cm … [Given in the question]
BC = 4 cm
Now, we have to construct the right-angled triangle by using the above values.
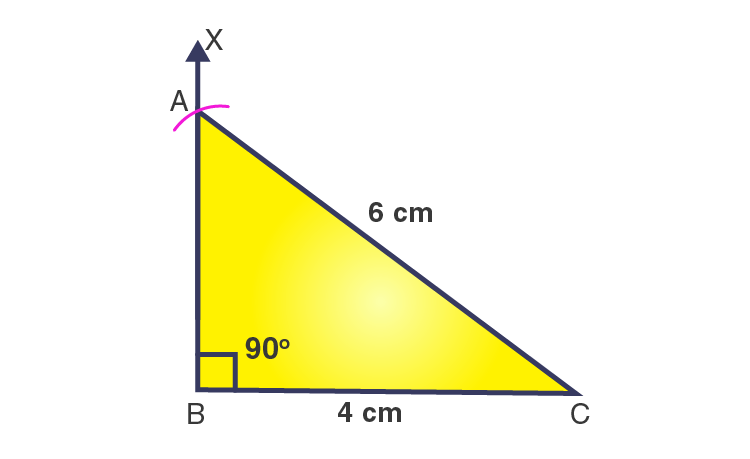
Steps of construction
1. Draw a line segment BC = 4 cm.
2. At point B, draw a ray BX to making an angle of 90o , i.e., ∠XBC = 90o .
3. With C as a centre and radius 6 cm, draw an arc that cuts the ray BX at A.
4. Join AC.
Then, ΔABC is the required right-angled triangle.
3. Construct an isosceles right-angled triangle ABC, where m∠ACB = 90° and AC = 6 cm.
Solution:-

Steps of construction
1. Draw a line segment BC = 6 cm.
2. At point C, draw a ray CX to making an angle of 90o , i.e., ∠XCB = 90o .
3. With C as a centre and radius 6 cm, draw an arc that cuts the ray CX at A.
4. Join AB.
Then, ΔABC is the required right-angled triangle.